Geometría (113). Ángulo máximo

Foto: Antonio Martínez Garcia (Correos, Madrid)

El problema que sigue es parte del Examen de Admisión a la Universidad UNI (Perú).
Lo he obtenido en https://plus.google.com/u/0/+RUBI%C3%91OS/posts/NugpUohBD8S
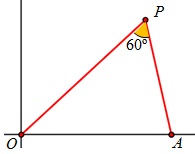
Su enunciado es el que se indica en el dibujo.

Viene solucionado en la página web de arriba.
Me parece un trabajo elogiable, pero hay un pequeño detalle que, aunque es cierto, no es evidente. (El autor afirma que puede demostrase, pero no se hace; posiblemente por aligerar el vídeo o porque el público al que va destinado no maneje con soltura la optimación). El detalle consiste en afirmar que la expresión x + 2/x es mínima cuando ambos sumandos son iguales, cosa que no demuestra.
Por mi parte, daré una solución distinta de la indicada en el vídeo, utilizando cuestiones de proporcionalidad, de trigonometría y de optimización.

También me he planteado qué pasaría si en cualquier universidad española se propusiese este problema en la prueba de acceso. (Mejor no contestamos).

Problema
Calcula el valor de x para que el ángulo theta sea máximo.

Solución.

Geometría (112). Lugar geométrico (II)

Foto: José María Martínez García

Los métodos de resolución de problemas suelen ser variados: geométricos, algebraicos, hacia atrás, por inducción,… La elección del método puede ser determinante para encontrar la solución; otras veces indica solamente una preferencia o una limitación (se sabe lo que se sabe), que genera soluciones elegantes, largas, complicadas, sencillas… Lo ideal es utilizar un método que lleve a encontrar una solución elegante y sencilla del problema. Pero, ¿cuál es ese método?, ¿y qué solución es la más sencilla?
El párrafo anterior viene a cuento porque aquí propongo nuevamente el mismo problema del post anterior, pero resolviéndolo por dos procedimientos distintos. Uno aplicando técnicas de optimización clásica, usando derivadas; el otro utilizando una fórmula trigonométrica. Sugiero al lector que haga lo mismo y que se pregunte cuál es la solución que prefiere.

Problema.
Sean los puntos O(0, 0) y A(1, 0). Se considera otro punto P(x, y) en el primer cuadrante de forma que el ángulo OPA mida 60º. Aplicando el cálculo diferencial y la trigonometría, halla el valor del ángulo alfa para que la suma de las longitudes OP + PA sea máxima.

Solución.

Geometría (111). Lugar geométrico

Foto: Carmen García Matas (Biblioteca Nacional, Madrid)

Es sorprendente la cantidad de resultados que se obtienen al teclear en Google la frase de Paul Klee; “A line is a dot that went for a walk” = "Una línea es un punto que fue a dar un paseo". Aparecen, además, una serie de vídeos que constituyen un divertimento para niños y mayores (dibujos, música,…). Por ejemplo:
https://www.youtube.com/watch?v=7kFoi2EiG9U; 
https://www.youtube.com/watch?v=cDyksXdhqV4;
https://www.youtube.com/watch?v=DQEVllmeWH4

Parafraseando a Paul Klee, me atrevo a decir que: “Un lugar geométrico es un punto que fue a dar un paseo siguiendo determinadas instrucciones”.
Sirva lo dicho como introducción para plantear el problema que sigue.

Problema.
Sean los puntos O(0, 0) y A(1, 0). Se considera otro punto P(x, y) en el primer cuadrante de forma que el ángulo OPA mida 60º. Encontrar la línea por la que puede moverse el punto. ¿Cuál será su ecuación?

Solución.

Geometría (110). Ángulos en la circunferencia

Foto: Juan Luís Cordero.

Como estamos en verano voy a permitirme el lujo (licencia había escrito en primer lugar) de escribir lo que me venga en gana.

Anoche asistí a la inauguración de una exposición de arte. Lleva el título de “Palimpsestos”, y en ella se exponen algunos collages de Emilio Gil. Está en la Sala de Exposiciones de la Oficina de Correos que hay en el edificio del Ayuntamiento de Madrid, en Cibeles.
Pues bien, entre los magníficos collages del artista, para que el observador sepa observar mejor lo expuesto, hay una serie de frases pedagógicas. Una de esas frases, de un tal Otl Aicher (para mi desconocido:  https://es.wikipedia.org/wiki/Otl_Aicher) me llamó la atención, pues me llevó a la Geometría y, si se me permite la cursilería, a la belleza, a la armonía. O quizá, y como dijo otro artista a lo “extensamente figurativo”, que a saber lo que significa.
Pero vayamos a la frase de Aicher. Dice así: “Entre dos puntos no hay ninguna relación establecida. Estén muy juntos o muy alejados entre sí, su distancia permanece sin comparación con nada. Si se señala un tercer punto, se distinguen tres distancias entre los tres puntos y éstas guardan ahora una relación: son iguales o son distintas, sus proporciones pueden quedar indeterminadas u ordenadas, es decir ordenadas según relaciones determinadas. Este es el origen de la estética”. 
Me sentí animado con el argumento, pues al “hacer geometría” me consideré un poco artista. (Sin exagerar, claro).

Los dos problemas que siguen son una sencilla e interesante aplicación de la propiedad de los ángulos inscritos. Además de a los lectores de este blog, puede interesar a los alumnos de 2º o 3º de ESO.

Problema 1
Demuestra que el ángulo x es la mitad de la suma de la amplitud de los arcos AB y CD.

Problema 2
Demuestra que el ángulo y es la mitad de la diferencia de la amplitud de los arcos AB y CD.

Solución.

Geometría (109). Tangentes comunes

Foto: Carmen Martínez García (Catedral de Ávila)

LIII OME - SEGUNDA PRUEBA FASE LOCAL, COMUNIDAD DE MADRID 21 de diciembre de 2016https://www.ucm.es/data/cont/media/www/pag-91362/olimpiada_53.pdf

El problema que sigue no es sencillo. Para resolverlo hay que conocer varias propiedades de las tangentes a una circunferencia; también se deben utilizar los teoremas de Tales y de Pitágoras… Me parece un buen entretenimiento veraniego para los alumnos mayores, y para profesores. Ánimo, y no veáis la solución antes de tiempo.

Problema. 
El dibujo muestra dos circunferencias y dos rectas tangentes a ambas, siendo A, B, P y Q los puntos de tangencia. Si la longitud del segmento PQ es 14 y la del AB es 16, calcula el producto de los radios de las circunferencias.

Solución.

Geometría (108). Cociente de áreas

Foto: Aitor Merinero (Río Tajo en Lisboa)

https://www.concursoprimavera.es/resources/problemas/problemas-2000-fase2-nivel4.pdf

Dos problemas fáciles. Para los más jóvenes… Pero hay que saber algunas fórmulas y pensar un poco.

Problema 1.
Con centro en O dibujamos el cuadrante OXY, siendo XY a su vez diámetro del semicírculo que se muestra en la figura. Si llamamos T, S y C a las áreas de las regiones que se indican en la figura, ¿cuál es el cociente T/C?

Problema 2.
En el triángulo rectángulo PQR de la figura, el ángulo P es de 45º y el arco de centro P y radio PR corta a PQ en S. ¿Cuál es el cociente entre el área de PRS y el área de RSQ?

Soluciones.

Geometría (107). Bisectrices

Foto: Cristina Martínez García (Ávila)

https://www.ucm.es/data/cont/media/www/pag-91362//enunciados%20LIII%20Fase%20cero.pdf
(LIII Olimpiada Matemática Española. Fase Cero).

El problema que se propone en este “post” no es sencillo, al menos hasta que se resuelve.
Esta idea ya la hemos comentado varias veces: los problemas de geometría pueden ser difíciles, pero solo hasta que se resuelven; pues entonces suelen verse con gran nitidez; y pensamos: ¿cómo no se me ha ocurrido antes?
Por mi parte confieso que su resolución no me ha llegado hasta el tercer intento. Y, por supuesto, he pensado: ¿cómo no lo habré visto antes?
Para su resolución debe utilizarse el teorema de la bisectriz (post 73 de este Blog)

Problema
En el triángulo ABC de la figura de lados AB = 6 cm, BC = 7 cm y CA = 8 cm, las bisectrices AD y BE de los ángulos A y B respectivamente, se cortan en el punto F. ¿Cuál es el cociente AF/FD?

Solución.

Geometría (106). Áreas de dos regiones

Foto: Antonio Martínez García

https://www.concursoprimavera.es/resources/problemas/problemas-2000-fase1-nivel3.pdf

Con frecuencia, algunos de los lectores de este blog me comentan: “no me sale ni uno de los problemas que propones”. Esta vez no me lo podrán decir, pues los dos problemas que siguen son muy fáciles. Ahí van:

Problema 1
En el rectángulo de la figura, la longitud PQ es doble de la QR, ST = 6 cm y TR = 12 cm. ¿Cuánto vale el área sombreada?

Problema 2
La altura del trapecio PQRS de la figura mide 6 cm; y sus bases, 10 y 4 cm. Si T es el punto medio de QR, ¿cuál es el área de la región sombreada?

Solución.