Geometría (108). Cociente de áreas

Foto: Aitor Merinero (Río Tajo en Lisboa)

https://www.concursoprimavera.es/resources/problemas/problemas-2000-fase2-nivel4.pdf

Dos problemas fáciles. Para los más jóvenes… Pero hay que saber algunas fórmulas y pensar un poco.

Problema 1.
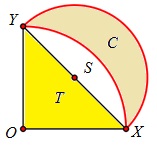
Con centro en O dibujamos el cuadrante OXY, siendo XY a su vez diámetro del semicírculo que se muestra en la figura. Si llamamos T, S y C a las áreas de las regiones que se indican en la figura, ¿cuál es el cociente T/C?

Problema 2.
En el triángulo rectángulo PQR de la figura, el ángulo P es de 45º y el arco de centro P y radio PR corta a PQ en S. ¿Cuál es el cociente entre el área de PRS y el área de RSQ?

Soluciones.

Geometría (107). Bisectrices

Foto: Cristina Martínez García (Ávila)

https://www.ucm.es/data/cont/media/www/pag-91362//enunciados%20LIII%20Fase%20cero.pdf
(LIII Olimpiada Matemática Española. Fase Cero).

El problema que se propone en este “post” no es sencillo, al menos hasta que se resuelve.
Esta idea ya la hemos comentado varias veces: los problemas de geometría pueden ser difíciles, pero solo hasta que se resuelven; pues entonces suelen verse con gran nitidez; y pensamos: ¿cómo no se me ha ocurrido antes?
Por mi parte confieso que su resolución no me ha llegado hasta el tercer intento. Y, por supuesto, he pensado: ¿cómo no lo habré visto antes?
Para su resolución debe utilizarse el teorema de la bisectriz (post 73 de este Blog)

Problema
En el triángulo ABC de la figura de lados AB = 6 cm, BC = 7 cm y CA = 8 cm, las bisectrices AD y BE de los ángulos A y B respectivamente, se cortan en el punto F. ¿Cuál es el cociente AF/FD?

Solución.

Geometría (106). Áreas de dos regiones

Foto: Antonio Martínez García

https://www.concursoprimavera.es/resources/problemas/problemas-2000-fase1-nivel3.pdf

Con frecuencia, algunos de los lectores de este blog me comentan: “no me sale ni uno de los problemas que propones”. Esta vez no me lo podrán decir, pues los dos problemas que siguen son muy fáciles. Ahí van:

Problema 1
En el rectángulo de la figura, la longitud PQ es doble de la QR, ST = 6 cm y TR = 12 cm. ¿Cuánto vale el área sombreada?

Problema 2
La altura del trapecio PQRS de la figura mide 6 cm; y sus bases, 10 y 4 cm. Si T es el punto medio de QR, ¿cuál es el área de la región sombreada?

Solución.

Geometría (105). Tangentes a circunferencia

Foto: Carmen García Matas (Madrid, El Retiro).

El problema que sigue se propuso en la Fase 0 de la LIII OLIMPIADA MATEMÁTICA ESPAÑOLA (Comunidad de Madrid).
No es un problema difícil, aunque tampoco inmediato. Para resolverlo hay que conocer una de las propiedades de las tangentes a una circunferencia desde un punto.
Puede proponerse a estudiantes de Bachillerato.

Problema
En el triángulo PQT de la figura, PQ = 10 cm, QT = 5 cm y el ángulo PQT = 60º. Los puntos Y, W y V son los puntos de tangencia de la circunferencia de centro O con las rectas que determinan los lados del triángulo. ¿Cuál es, en cm, el radio de dicha circunferencia?

Solución.

Geometría (104). Región circular

Foto: José María Martínez García (Varsovia)

https://www.concursoprimavera.es/resources/problemas/problemas-2003-fase2-nivel4.pdf

El problema que sigue es relativamente sencillo. Pueden hacerlo los alumnos de 3º de ESO; y de 2º si tienen interés.
Para resolverlo solo es necesario conocer las fórmulas de las superficies de regiones circulares y algo de triángulos.

Problema
Los centros de dos círculos iguales de radio 6 distan entre sí 6 · (raíz de 3). ¿Cuál es el área de la región común a ambos?

Solución.

Geometría (103). Ángulo alfa

Foto: Antonio Martínez García (Universidad de Alcalá de Henares)

El problema que se plantea a continuación es fácil de entender aunque, posiblemente, difícil de solucionar. No requiere conocimientos especiales, pero exige varios pasos intermedios que puede que no se encadenen adecuadamente. Pienso que es un reto bonito.
Para su resolución es conveniente recordar la propiedad de los ángulos inscritos en una circunferencia.  

Problema
El triángulo ABC es isósceles, con ángulo A de 20º. Con centros en B y C se trazan ángulos de 50º y 60º y se marcan los puntos D y E sobre los lados AB y AC, respectivamente. ¿Cuánto mide el ángulo DEC?

Solución.

Geometría (102). Circunferencia inscrita

Foto: José María Martínez García (Puerto Rico)

X CONCURSO DE PRIMAVERA DE MATEMÁTICAS (2006, Nivel III, 2º Fase)
https://www.concursoprimavera.es/resources/problemas/problemas-2006-fase2-nivel3.pdf

El problema que sigue se planteó a los alumnos de 3º y 4º de ESO. Puede servir para recordar la relación entre los distintos “centros” (baricentro, incentro…) en los triángulos equiláteros.
Para el baricentro puede verse la entrada nº 13 de este Blog.

Problema
El perímetro de un triángulo equilátero coincide numéricamente con el área de su círculo inscrito. ¿Cuál es el radio de este círculo?

Solución.

Geometría (101). Semicircunferencia

Foto: Carmen García Matas (Mediterráneo en Daimuz)

IV CONCURSO DE PRIMAVERA DE MATEMÁTICAS (2000, Nivel III, 2º Fase).
https://www.concursoprimavera.es/resources/problemas/problemas-2000-fase2-nivel3.pdf

El problema que sigue se planteó a los alumnos de 3º y 4º de ESO. Puede servir para recordar los teoremas del cateto y de la altura.

Problema
En la semicircunferencia de la figura, con centro O, OM = 3 · MQ y RM es perpendicular a PQ. ¿Cuál es el cociente PR/RM?

Solución.