Geometría (105). Tangentes a circunferencia

Foto: Carmen García Matas (Madrid, El Retiro).

El problema que sigue se propuso en la Fase 0 de la LIII OLIMPIADA MATEMÁTICA ESPAÑOLA (Comunidad de Madrid).
No es un problema difícil, aunque tampoco inmediato. Para resolverlo hay que conocer una de las propiedades de las tangentes a una circunferencia desde un punto.
Puede proponerse a estudiantes de Bachillerato.

Problema
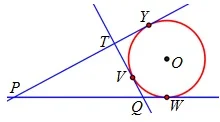
En el triángulo PQT de la figura, PQ = 10 cm, QT = 5 cm y el ángulo PQT = 60º. Los puntos Y, W y V son los puntos de tangencia de la circunferencia de centro O con las rectas que determinan los lados del triángulo. ¿Cuál es, en cm, el radio de dicha circunferencia?

Solución.

Geometría (104). Región circular

Foto: José María Martínez García (Varsovia)

https://www.concursoprimavera.es/resources/problemas/problemas-2003-fase2-nivel4.pdf

El problema que sigue es relativamente sencillo. Pueden hacerlo los alumnos de 3º de ESO; y de 2º si tienen interés.
Para resolverlo solo es necesario conocer las fórmulas de las superficies de regiones circulares y algo de triángulos.

Problema
Los centros de dos círculos iguales de radio 6 distan entre sí 6 · (raíz de 3). ¿Cuál es el área de la región común a ambos?

Solución.

Geometría (103). Ángulo alfa

Foto: Antonio Martínez García (Universidad de Alcalá de Henares)

El problema que se plantea a continuación es fácil de entender aunque, posiblemente, difícil de solucionar. No requiere conocimientos especiales, pero exige varios pasos intermedios que puede que no se encadenen adecuadamente. Pienso que es un reto bonito.
Para su resolución es conveniente recordar la propiedad de los ángulos inscritos en una circunferencia.  

Problema
El triángulo ABC es isósceles, con ángulo A de 20º. Con centros en B y C se trazan ángulos de 50º y 60º y se marcan los puntos D y E sobre los lados AB y AC, respectivamente. ¿Cuánto mide el ángulo DEC?

Solución.

Geometría (102). Circunferencia inscrita

Foto: José María Martínez García (Puerto Rico)

X CONCURSO DE PRIMAVERA DE MATEMÁTICAS (2006, Nivel III, 2º Fase)
https://www.concursoprimavera.es/resources/problemas/problemas-2006-fase2-nivel3.pdf

El problema que sigue se planteó a los alumnos de 3º y 4º de ESO. Puede servir para recordar la relación entre los distintos “centros” (baricentro, incentro…) en los triángulos equiláteros.
Para el baricentro puede verse la entrada nº 13 de este Blog.

Problema
El perímetro de un triángulo equilátero coincide numéricamente con el área de su círculo inscrito. ¿Cuál es el radio de este círculo?

Solución.

Geometría (101). Semicircunferencia

Foto: Carmen García Matas (Mediterráneo en Daimuz)

IV CONCURSO DE PRIMAVERA DE MATEMÁTICAS (2000, Nivel III, 2º Fase).
https://www.concursoprimavera.es/resources/problemas/problemas-2000-fase2-nivel3.pdf

El problema que sigue se planteó a los alumnos de 3º y 4º de ESO. Puede servir para recordar los teoremas del cateto y de la altura.

Problema
En la semicircunferencia de la figura, con centro O, OM = 3 · MQ y RM es perpendicular a PQ. ¿Cuál es el cociente PR/RM?

Solución.

Geometría (100). Con regla y compás (II)

Foto: Caty Martínez García. (Madrid)

Esta entrada es la número 100. Me parece un número suficientemente significativo para que nos felicitemos todos.
El problema que sigue no es fácil, aunque habría que poner la coletilla de siempre, “hasta que se resuelve”. Es lo que pasa con los problemas de regla y compás: cuando se han resuelto parecen evidentes; pero hasta que se consigue puede pasar de todo.
Su enunciado ha aparecido en una vieja carpeta de hace más de 30 años. Allí tengo apuntadas unas referencias que he sido incapaz de localizar; dicen: Problema 47 (p.66) de “Problemas de Geometría”, J.M. Gómez Per…(no leo bien el segundo apellido). Con mi agradecimiento.

Problema
Dadas tres rectas paralelas, trazar un triángulo equilátero con vértices en cada una de las rectas.

Solución.

Geometría (99). Triángulos equiláteros

Foto: Adrián Santos

IX CONCURSO DE PRIMAVERA DE MATEMÁTICAS (2005, Nivel IV, 2º Fase)
https://www.concursoprimavera.es/resources/problemas/problemas-2005-fase2-nivel4.pdf

El problema que sigue se planteó a los alumnos de Bachillerato en el Concurso de Primavera. Su solución es muy fácil aplicando la noción de seno de un ángulo. Y es más fácil si se piensa un poco, cosa que no ha hecho el que suscribe; aunque después he completado el asunto.
Mi solución no coincidía con ninguna de las cinco dadas en el examen, pero dadoel cuidado con el que preparan las pruebas los organizadores del Concurso me he planteado hacerlas coincidir. Así ha sido; pero después, pensando un poco más, he dado con la solución casi inmediata, supongo que erala prevista por los organizadores.

Problema
El triángulo ABC de lados correspondientes a, b y c tiene un ángulo en A de 120º. Por ello podemos obtener girando, el triángulo equilátero BCD formado por tres triángulos como el de partida y un triángulo equilátero pequeño interior AEF. ¿Cuál es el área de este triángulo equilátero AEF?

Solución.

Geometría (98). Con compás (I)

Foto: Antonio Martínez García

El problema que planteo es un clásico "de regla y compás". En estos problemas es frecuente que “la idea” sea decisiva. Y más frecuente aún es que cuando esté resuelto parezca una obviedad. Algo de eso pasa aquí. Se trata de un problema sencillo cuando se ha resuelto.
Puede proponerse a los alumnos de bachillerato, aunque podría ponerse desde 2º de ESO, pues los conocimientos que se precisan son elementales para los seguidores de este blog: teorema de Tales; perpendicularidad; paralelismo…; que la distancia de un punto a una recta es la menor de las distancias posibles, la que hay entre el punto dado y su proyección (perpendicular) sobre la recta.
Por cierto, hay dos soluciones.

Problema
Dado un punto A sobre el lado r de un ángulo, encontrar otro punto B en el mismo lado que equidiste de A y del otro lado s.

Solución.