Foto: Carmen García Matas (presa de El Villar, Madrid)
El problema que sigue lo he visto propuesto en l libro Geometría, de Puig Adam (Madrid 1944).
No es inmediato, aunque (cuando se ha resuelto) se entiende fácilmente.
Puede proponerse a los alumnos y profesores de Secundaria.
Problema
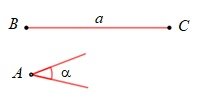
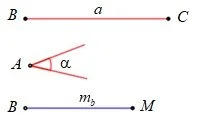
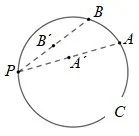
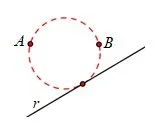
Determina el lugar geométrico de los incentros de los triángulos con un lado fijo y un ángulo opuesto constante.