Geometría (69). Triángulos

Foto: Carmen García Matas (Mediterráneo en Valencia)

XIX Concurso de Primavera de Matemáticas (2015)
http://www.sociedadpuigadam.es/primavera/problemas/2015/2015_2_nivel4.pdf

El problema que sigue es muy sencillo. Se propuso a alumnos de Bachillerato pero puede hacerlo cualquier alumno de Secundaria, pues basta con conocer las cuestiones básicas de Geometría.

Problema
En el rectángulo ABCD de la figura, AB = 2 y BC = 1. Si tanto ABX como BCY son triángulos equiláteros, ¿cuál es el área de la zona sombreada?

Solución.

Geometría (68). Círculos

Foto: Carmen Martínez García (Cantabria)

XIV Olimpiada Matemática de Albacete (2003)
http://scmpm.blogspot.com.es/p/problemas-de-la-olimpiada-matematica.html

El problema que sigue es relativamente sencillo. Se ha propuesto para alumnos de 13 y 14 años. Creo que es entretenido para esta época del año: en España estamos empezando las vacaciones veraniegas. Requiere conocimientos básicos de geometría: triángulos equiláteros, Pitágoras, propiedad del incentro y circunferencia inscrita…

Problema
Conocido el valor (L) del lado del triángulo equilátero, calcula:
a) Los radios R y r.                                        b) El área de cada círculo.
c) La relación entre el área sombreada respecto del área del triángulo.

Solución.

Geometría (67). Uve

Foto: Adrián Santos López (Auñón, Guadalajara)

Del XX Concurso de Primavera de Matemáticas (1ª Fase, Nivel IV)
http://www.sociedadpuigadam.es/primavera/problemas/2016/2016_1_nivel4.pdf

El problema que sigue es relativamente sencillo. Podría plantearse a alumnos de cualquier nivel. Solo deben tener la noción de semejanza y conocer cómo se calculan las áreas de las figuras planas elementales.

Problema
En el cuadrado de la figura, de lado 20 cm, hemos dibujado esta “V” con las dimensiones que se indican.  ¿Cuál es el área, en cm2, que ocupa la letra “V”? 

Solución.

Geometría (66). Trapecio

Foto: Carmen García Matas (El Escorial)

Del XX Concurso de Primavera de Matemáticas (2ª Fase, Nivel IV)
http://www.sociedadpuigadam.es/primavera/problemas/2016/2016_2_nivel4.pdf

El problema que sigue no es difícil. Podría plantearse a alumnos de 3º o 4º de ESO, incluso a los de 2º de ESO.
Para su resolución hay que recordar cómo va lo de la razón de proporcionalidad entre longitudes y superficies en las figuras semejantes. Y, como siempre, lo imprescindible es tener interés por resolverlo.

Problema
En el triángulo isósceles PQR de la figura, en el QP = 150 y PR = QR = 125, hay  tres segmentos paralelos a QR que lo dividen en cuatro regiones de igual área. ¿Cuánto vale la altura h del trapecio inferior? 

Solución.

Geometría (65). Cuadrado

Foto: José María Martínez García (Ávila)

Del XIX Concurso de Primavera de Matemáticas (2ª Fase, Nivel IV) 
http://www.sociedadpuigadam.es/primavera/problemas/2015/2015_2_nivel4.pdf

El problema que sigue es relativamente sencillo. Puede proponerse a alumnos de cualquier nivel de Secundaria. Para su resolución solo es necesario hacer pequeños arreglos con las figuras, buscando o definiendo otras que nos permitan establecer relaciones entre sus lados.

Problema
La figura adjunta muestra un rectángulo ABCD inscrito en una semicircunferencia  y su diámetro. las dimensiones del rectángulo son AB = 12 y BC = 28. Se ha construido un cuadrado DEFG como ves en la figura. ¿Cuánto vale el área del cuadrado DEFG?

Solución.

(Geometría (64). Lentes

Foto: Caty Martínez (París)

Del XX Concurso de Primavera de Matemáticas (2ª Fase, Nivel IV)
http://www.sociedadpuigadam.es/primavera/problemas/2016/2016_2_nivel4.pdf

Los lectores de este blog saben que no busco problemas complicados o que requieran algún aparato matemático más allá de los niveles de ESO; también procuro huir de la trigonometría. Mi objetivo es recopilar una serie de problemas que puedan estimular la afición a la Geometría entre los jóvenes estudiantes. Algo conseguiremos entre todos.
El problema que sigue se propuso hace unos meses a los alumnos de bachillerato participantes en el Concurso de Primavera de Matemáticas. Pienso que no es difícil, pero es posible que no se vea a la primera; en ese caso, deben buscarse alternativas gráficas, recordar otros problemas similares...,  dejarlo para otro momento, aunque sin rendirse, pues el problema es asequible para alumnos de 3º de ESO en adelante.

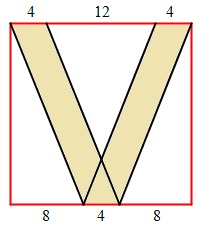
Problema
La primera  imagen de don  Retorcido es una caricatura que le hicieron hace 20 años (cuando comenzaron los Concursos de Primavera). Está enmarcada en un cuadrado de 6 dm de lado, la nariz es un triángulo equilátero y cada lente, circular, es tangente a dos lados del marco y a un lado de la nariz. ¿Cuánto mide el radio del círculo que representa cada lente?

Solución.

Geometría (63). Semicircunferencia

Foto: Adina Marín (Sevilla)

Del X Concurso de Primavera de Matemáticas (2ª Fase, Nivel IV)
http://www.sociedadpuigadam.es/primavera/problemas/2006/2006_2_nivel4.pdf

El problema que sigue se propuso hace algunos años a los alumnos de bachillerato participantes en el Concurso de Primavera de Matemáticas. Pienso que tiene un nivel de dificultad medio, aunque a mí me ha salido al segundo intento: lo tuve que dejar para otro día, pues durante un buen rato no fui capaz de “ver” una solución no trigonométrica. La solución que puede calificarse de fácil es asequible para alumnos de 3º de ESO (14 o 15 años), pues para encontrarla solo se requiere saber hallar el área de un triángulo y algo de ángulos inscritos.

Problema
En el semicírculo de la figura, de diámetro AD = 4, inscribimos el cuadrilátero ABCD con AB = BC = 1. ¿Cuánto mide el lado CD?

Solución.

Geometría (62). Sector

Foto: Cristina Martínez García. (Museo del ferrocarril, Madrid)

Del X Concurso de Primavera de Matemáticas (2ª Fase, Nivel IV).
http://www.sociedadpuigadam.es/primavera/problemas/2006/2006_2_nivel4.pdf

Este problema se propuso hace unos años a los alumnos de bachillerato participantes en el Concurso de Primavera de Matemáticas. Pienso que tiene un nivel de dificultad medio, aunque podría proponerse a partir de 3º de ESO (14 o 15 años). Para su resolución se necesita, como tantas veces, conocer los dos teoremas básicos de la Geometría: Pitágoras y Tales.

Problema
En la figura que te mostramos, el cociente  entre el radio del sector y el del círculo inscrito en ese sector es 3. ¿Cuál es el cociente entre el área del sector y el área del círculo?

Solución.