Geometría (61). Trapecio

Foto: José María Martínez García (Desierto de Arabia)

Del XIII Concurso de Primavera de Matemáticas.
http://www.sociedadpuigadam.es/primavera/problemas/2009/2009_2_nivel4.pdf

Después de un par de problemas más o menos complicados vuelvo a otro sencillo.
Para su resolución se requiere conocer solamente el área de un triángulo y la relación de Tales entre triángulos semejantes.
Podría proponerse a alumnos de 2º de ESO, indicándoles, además, que comprobasen que el resultado obtenido es correcto, haciendo por separado el área del triángulo y la del trapecio. (Es posible que esa comprobación suponga para los alumnos una dificultad mayor).

Problema
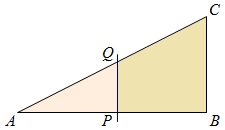
En el triángulo rectángulo ABC de la figura, el cateto AB tiene longitud 3. Por el punto P, trazamos una paralela a BC que corta a la hipotenusa AC en el punto Q. Si el área del trapecio PBCQ es el doble que el área del triángulo PQA, ¿cuánto mide AP?

Solución.

Geometría (60). Cociente de superficies

Foto: Catalina Martínez García (Gangas de Onís, Asturias)

De la XLII Olimpiada Matemática Española (Fase local, Comunidad de Madrid)

El problema que propongo en este post tampoco es sencillo; al menos, a mí no me ha resultado fácil. Además, aunque puedo dar tres formas de solucionarlo no he conseguido la que realmente pretendía, pues mi intención inicial era resolverlo comparando gráficamente las superficies que se proponen, digamos una respuesta de marquetería: dividendo las superficies triangulares, pegando unas partes a otras…
La primera solución la he encontrado con ayuda del álgebra. Creo que es un tanto artificiosa, quizá nada sencilla.
También puede darse otra solución trigonométrica más sencilla, lo que permite poner de manifiesto la potencia de la trigonometría.
Por último, sin buscarla, encontré una tercera solución; quizá la más sencilla
Podría recomendarse a alumnos de bachillerato.

Problema
En la siguiente figura, ABCD es un cuadrado y BEF un triángulo equilátero. ¿Cuál es el cociente  entre el área del triángulo DEF y el área del triángulo ABE?

Solución.

Geeometría (59) Taladro

Foto: Adina Marín (Vaticano)

Este problema es distinto a los últimos que he propuesto. Hay que advertir que no faltan datos y que el volumen que se pide es un número concreto.
Puede proponerse a alumnos de 2º de bachillerato; o a más jóvenes si se les da el volumen de un casquete esférico (fórmula que no es frecuente conocer de memoria).
Buscando un gráfico apropiado en Internet (que no he encontrado) he visto que es un problema que circula por la red, incluso se dice que es muy sencillo. Puede que sea así, pero yo he necesitado deducir la fórmula de uno de los casquetes esféricos que desaparecen de la esfera inicial: lo he hecho mediante una integral, por cierto, muy sencilla si se sabe hacer.

Problema
Se taladra diametralmente una esfera. Si el agujero cilíndrico tiene 6 cm de altura, ¿cuánto vale el volumen del trozo de esfera que queda?

Solución.

Geometría (58) Doblado

Foto: Carmen García Matas, (Madrid, Retiro)

Del XI Concurso de Primavera (Madrid, 2007)
http://www.sociedadpuigadam.es/primavera/problemas/2007/2007_2_nivel3.pdf

Otro problema relativamente sencillo. En la solución propongo dos formas de resolverlo; supongo que habrá alguna más. Ánimo y a por él.
Puede proponerse a alumnos de 3º de ESO en adelante.

Problema
Una hoja cuadrada de papel de 12 cm2 de área, es blanca por una cara y roja por la otra. Doblamos una esquina de la hoja formando un triángulo con dos lados paralelos a los lados de la hoja, como se muestra en la figura. Si ahora la superficie visible de la hoja es la mitad roja y la mitad blanca, ¿cuál es, en cm, la longitud del doblez EF?

Solución.

Geometría (57) Segmento

Foto: Catalina Martínez García (Lagos de Covadonga)

Del VI Concurso de Primavera (Madrid, 2002)
http://www.sociedadpuigadam.es/primavera/problemas/2002/2002_2_nivel4.pdf

Este problema es ligeramente más difícil que los anteriores, aunque solo requiere conocer un resultado clásico de Geometría: el teorema de la altura. (Si no lo recuerdas pincha aquí).
Puede proponerse a alumnos de 3º de ESO en adelante.

Problema
Sea AB un segmento de longitud 26 y C y D dos puntos en él tales que AC = 1 y AD = 8. Sean E y F dos puntos en una de las semicircunferencias de diámetro AB tales que EC y FD son perpendiculares a AB. Calcula EF.

Solución.

Geometría (56). Circunferencia inscrita

Foto: Adina Marín (Roma)

De la XLIX OLIMPIADA MATEMÁTICA ESPAÑOLA (Madrid, 2012)

Vuelvo a proponer otro problema relativamente sencillo; pero pienso que es bonito. Cualquier alumno (o profesor) que consiga resolverlo tendrá una pequeña satisfacción: de eso se trata.
Para resolverlo hay que conocer tres o cuatro cosas de geometría básica: la propiedad de la tangente a una circunferencia, manejar cuestiones de ángulos y de polígonos regulares, semejanza, Pitágoras…
Me gustaría acertar si digo que cualquier alumno de 2º de ESO debe estar en condiciones de hacerlo.

Problema
La circunferencia de la figura está inscrita en el cuadrilátero ABCD, siendo R, S, T y U los puntos de tangencia con los lados. Si el ángulo A =  90º, DR = 3 y el arco RST es de 210º, halla el área del círculo. 

Solución.

Geometría (55). Cuadrados

Foto: Adrian Santos López

XII Concurso de Primavera de Matemáticas (Madrid, 2008)
http://www.sociedadpuigadam.es/primavera/problemas/2008/2008_2_nivel4.pdf

El problema que sigue es relativamente sencillo. Aunque se propuso a alumnos de bachillerato puede hacerse a partir de 2º de ESO, pues basta con aplicar el teorema de Pitágoras.

Problema
El cuadrado ABCD de la figura mide 4 cm de lado y el cuadrado AEFG, 2 cm de lado. ¿Cuál es, en cm, la longitud de CE?

Solución.

Geometría (54). Galletas

Foto: Adina Marín, Roma

De la Olimpiada de Albacete

De la Olimpiada de Albacete
http://scmpm.blogspot.com.es/p/problemas-de-la-olimpiada-matematica.html

El problema que sigue es muy sencillo. Pienso que puede resolverlo cualquier estudiante de ESO (a partir de 12 años). Espero que sea así. Para su resolución necesitas conocer Pitágoras y hacer otro dibujo sobre las “galletas”.

Problema
Hemos colocado tres galletas totalmente circulares e iguales dentro de una caja rectangular, de forma que son tangentes entre sí y tangentes a las paredes de la caja que las alberga. Determina la proporción entre los lados de la caja.

Solución.