Foto: Cristina Martínez García (Catedral de Palma de Mallorca)
El problema que sigue es relativamente sencillo; adecuado para alumnos de 13 o 14 años. Puede servir para trabajar con ángulos inscritos en una circunferencia; y para aplicar los teoremas de Tales y Pitágoras.
Problema
El semicírculo grande tiene radio 2. Halla el área de cada uno de los semicírculos pequeños (son inscritos a los triángulos que se observan).
Foto: José Luis Quintero (Recópolis, Guadalajara)
El problema que sigue es bastante sencillo; adecuado para alumnos de 13 o 14 años. Puede servir para trabajar con ángulos inscritos en una circunferencia; y para aplicar Tales y Pitágoras.
Problema
Halla el área de la parte sombreada en el semicírculo de radio 2.
Foto: Carmen Martínez García (Mancha Real, Jaén)
El problema que sigue se propuso en el XXI Concurso de Primavera de Matemáticas (1ª Fase, nivel IV):
ttps://www.concursoprimavera.es/#problemas.
Aunque se propuso a estudiantes de Bachillerato puede plantearse a alumnos más jóvenes, de 13 o 14 años. Para su resolución hay que conocer la propiedad que cumplen los radios de dos circunferencias tangentes, y aplicar el teorema de Pitágoras.
Problema
El dibujo muestra un cuarto de circunferencia de radio 2 y dos semicircunferencias tangentes. ¿Cuál es el radio de la semicircunferencia pequeña?
Foto: MIguel Quintero Goicoechea (Desde Tailandia)
Se trata de un problema fácil, siempre que se vea geométricamente.
Si visualmente no se encuentra la solución se necesitará aplicar Pitágoras. En este caso, la solución sigue siendo fácil, aunque resulta más engorrosa. (Aplicando Pitágoras podría proponerse como ejercicio encontrar el lado del octógono).
Problema
La parte sombreada del octógono regular tiene área 50. ¿Cuánto mide el área del octógono?
Foto: José María Martínez García (en Chipre)
Para resolver el problema que sigue deben conocerse, y saber aplicar, los teoremas de Tales y Pitágoras.
Problema
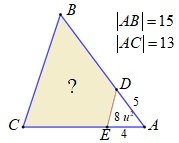
En el triángulo ABC, se tiene que AB = 15 y AC = 13. Sobre AB y AC se toman los puntos D y E, respectivamente, tales que AD = 5 y AE = 4. Si el área del triángulo ADE vale 8, halla la longitud del lado BC y el área del cuadrilátero DBCE.
Foto: Antonio Martínez García (Río Li en Guilin, China)
Problema extraído de la XXIX Olimpiadas Costarricense de Matemáticas (año 2017):
https://tecdigital.tec.ac.cr/revistamatematica/Libros/OLCOMA2019/XXIX%20OCM%202017.pdf
Aunque se trata de un problema fácil, tiene el inconveniente de que los alumnos no suelen conocer la propiedad del baricentro (punto de corte de las medianas).
El problema original se propone sin el dibujo que se da aquí. Pienso que es más interesante plantearlo sin dibujo y pedir a los estudiantes que lo hagan.
Problema
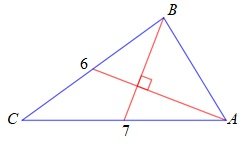
En el triángulo ABC, las medianas desde A y B se cortan perpendicularmente. Si AC = 7 y BC = 6, ¿cuánto vale AB?