Foto: Carmen Martínez García (Noruega)
Al resolver el problema propuesto en el Post 72 me topé con una solución que utiliza el teorema de la bisectriz y el teorema de Ceva.
En el Post 73 se propuso como problema el teorema de la bisectriz; en este propondré una de las variantes del teorema de Ceva. (Para el lector interesado, en Internet se puede encontrar bastante información sobre el asunto).
La demostración que propongo no es difícil, pero tampoco elemental. Digamos que hay que tener un interés notable para, en los tiempos que corren, afrontarla y dedicarle un par de horas para conseguir hacerla (no para estudiarla, que eso se hace en 10 minutos).
Para tal propósito he necesitado:
1) Hallar las superficies de algunos de los triángulos que aparecen en el dibujo.
2) Establecer la razón entre sus bases y sus superficies.
3) Utilizar alguna de las propiedades de las proporciones: En concreto: “si se tiene una serie de razones iguales, la suma (diferencia?) de los antecedentes partido por la suma de los consecuentes es igual a cualquiera de las razones”. Esto es: si a/b = c/d = k, entonces (a + c)/(b + d) = k.
4) Multiplicar las razones que aparecen en el enunciado que propongo a continuación y comprobar que su producto es 1.
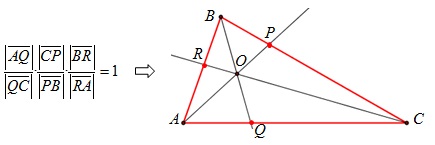
Problema: Demuestra el teorema de Ceva
Sean A, B, C vértices de un triángulo y los puntos P, Q, R en sus respectivos lados opuestos. Si las rectas AP, BQ y CR son concurrentes entonces se verifica que: