Geometría (3) Ángulos

March 10, 2015

Foto: Adrán Santos Lopez
Del Concurso de Primavera de Matemáticas 1ª Fase (varios años). Madrid

Los problemas que se proponen a continuación son muy sencillos. Para resolverlos basta con saber:
1)   La suma de los ángulos de cualquier triángulo vale 180º.
2)   Si una recta corta a otras paralelas, los ángulos que determina con todas ellas son iguales. Esto implica que los ángulos de lados paralelos son iguales o suplementarios.
3)   En un triángulo isósceles, los ángulos determinados por el lado desigual son iguales.

Problema 1
¿Cuál es el valor del ángulo x en la siguiente figura?

Problema 2
Las rectas horizontales son paralelas. ¿Cuánto vale x?

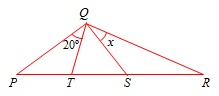
Problema 3
El dibujo de la derecha, que no está hecho a escala, se verifica que PT = QT = TS, QS = SR y el ángulo PQT = 20º. ¿Cuál es el valor de x?

Soluciones

Comment

Problema de geometría (2) De Pitágoras a Tales

February 28, 2015

PREMIO EXTRAORDINARIO DE EDUCACIÓN SECUNDARIA OBLIGATORIA DE LA COMUNIDAD DE MADRID. CURSO 2012–2013
SEGUNDO EJERCICIO: MATEMÁTICAS B
PROBLEMA 2

Se tienen dos circunferencias exteriores de centros C1 y C2 y radios 2 cm y 7 cm. La tangente que las deja debajo y es común a ambas corta a la recta que une dichos centros en un punto P. El segmento T1T2, cuyos extremos son los dos puntos de tangencia, mide 12 cm.
a) Haz un dibujo que refleje la situación y explica por qué la tangente a la circunferencia en un punto es perpendicular al radio.
b) Calcula la distancia entre los centros de las circunferencias.
c) Calcula la longitud del segmento PT2

La situación ahora cambia: la tangente común atraviesa la línea de los centros entre C1 y C2
d) Haz un dibujo que refleje la situación y calcula la distancia entre los centros.
(Observación para el lector: C1 debería ser C sub 1; y lo mismo para C2, T1 y T2).

Solución:

Comment

3 Comments

Problema de Geometría

February 22, 2015

Sabido es que la Geometría dejó de enseñarse en la Enseñanza Secundaria hace muchos años. El resultado del problema que he propuesto en el examen de hoy a mis alumnos (de 1º de Bachillerato de Ciencias, que es un grupo normal tirando a bueno) es un indicador elocuente.

El problema dice así:

Las bases de un trapecio miden 11 y 6 cm; otro de sus lados mide 4 cm y el ángulo que forman las dos rectas que contienen a los lados no paralelos es de 90º. Calcula el área del trapecio.

Comentario inicial
Al leer el problema varios alumnos no entendían lo de “las dos rectas que contienen a los lados no paralelos”; o no sabían cuáles eran esos lados. Otros, no recordaban cómo se calculaba el área de un trapecio. Me he visto en la necesidad de hacer un dibujo en la pizarra trazando las rectas que contienen a los lados no paralelos.

Solución.

3 Comments